LRC AC Circuits

1 Introduction

Previously, we have examined circuits with either capacitors and resistors or inductors and resistors powered by batteries that produce constant voltage. These are called direct current (DC) circuits. When a switch was closed to complete a circuit, the current varied in time, and the time dependence was exponential (the current had a term $e^{-t/\tau }$).

If we use a voltage source that varies in time sinusoidally instead of a battery, the current will also vary in time sinusoidally, possibly with a different phase. There will also be a “transient” exponential variation for a short amount, but here we only discuss the variation after the transient variation is zero “steady state.”

1.1 R Only

Figure (a) below shows a circuit in which an AC power source causes the current to vary sinusoidally in time according to $i(t)=I\cos (\omega t)$. By Ohm’s law, the equation for the instantaneous voltage across the resistor is $v_R(t)=IR\cos (\omega t)=V_R\cos (\omega t)$, where $V_R$ is the amplitude of the voltage source.

Figure (b) shows the time variation of current and voltage for this circuit. The voltage and current are “in phase” because the peaks, valleys, and zero crossings of $i(t)$ and $v_R(t)$ occur at the same time.

1.2 L Only

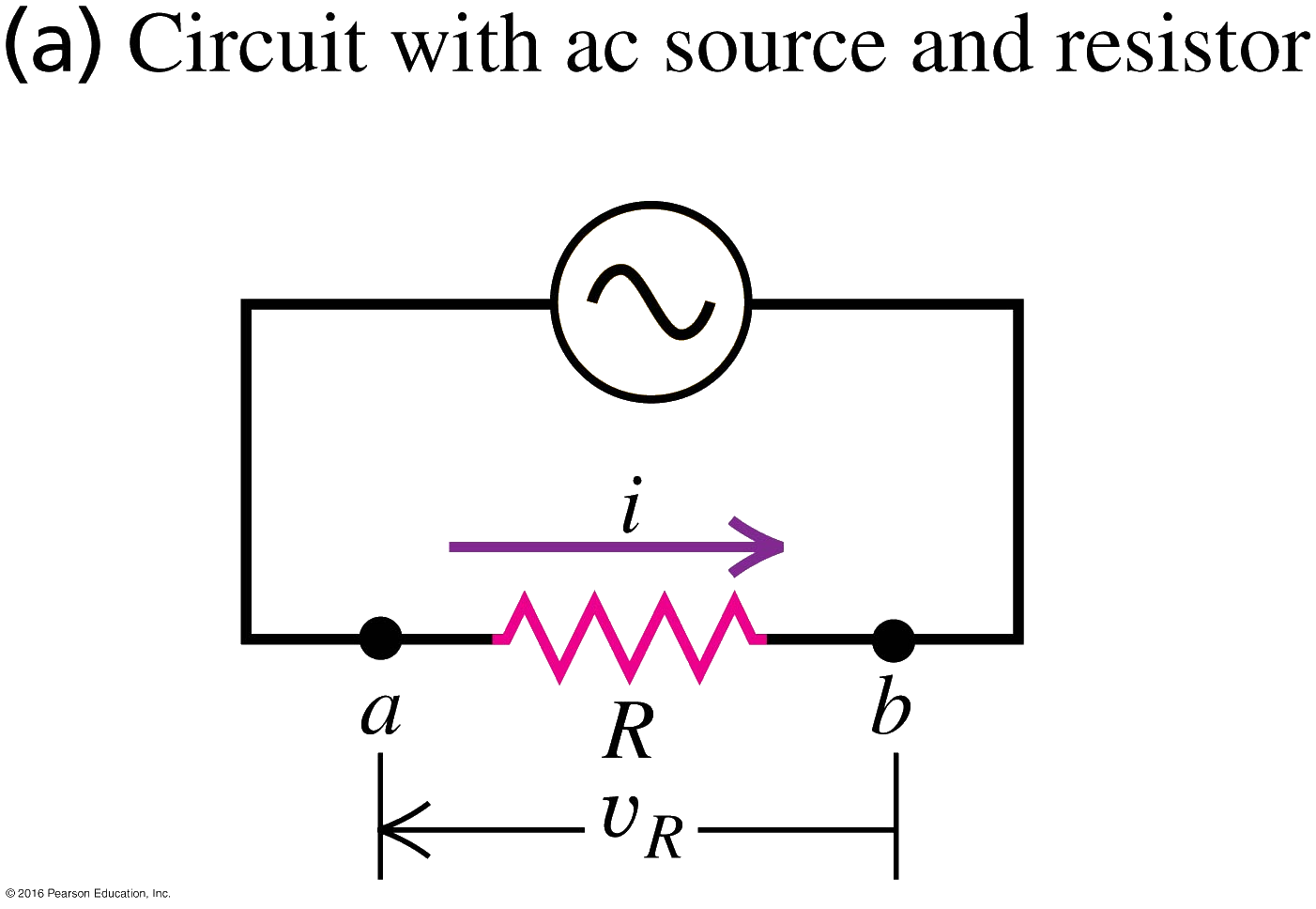
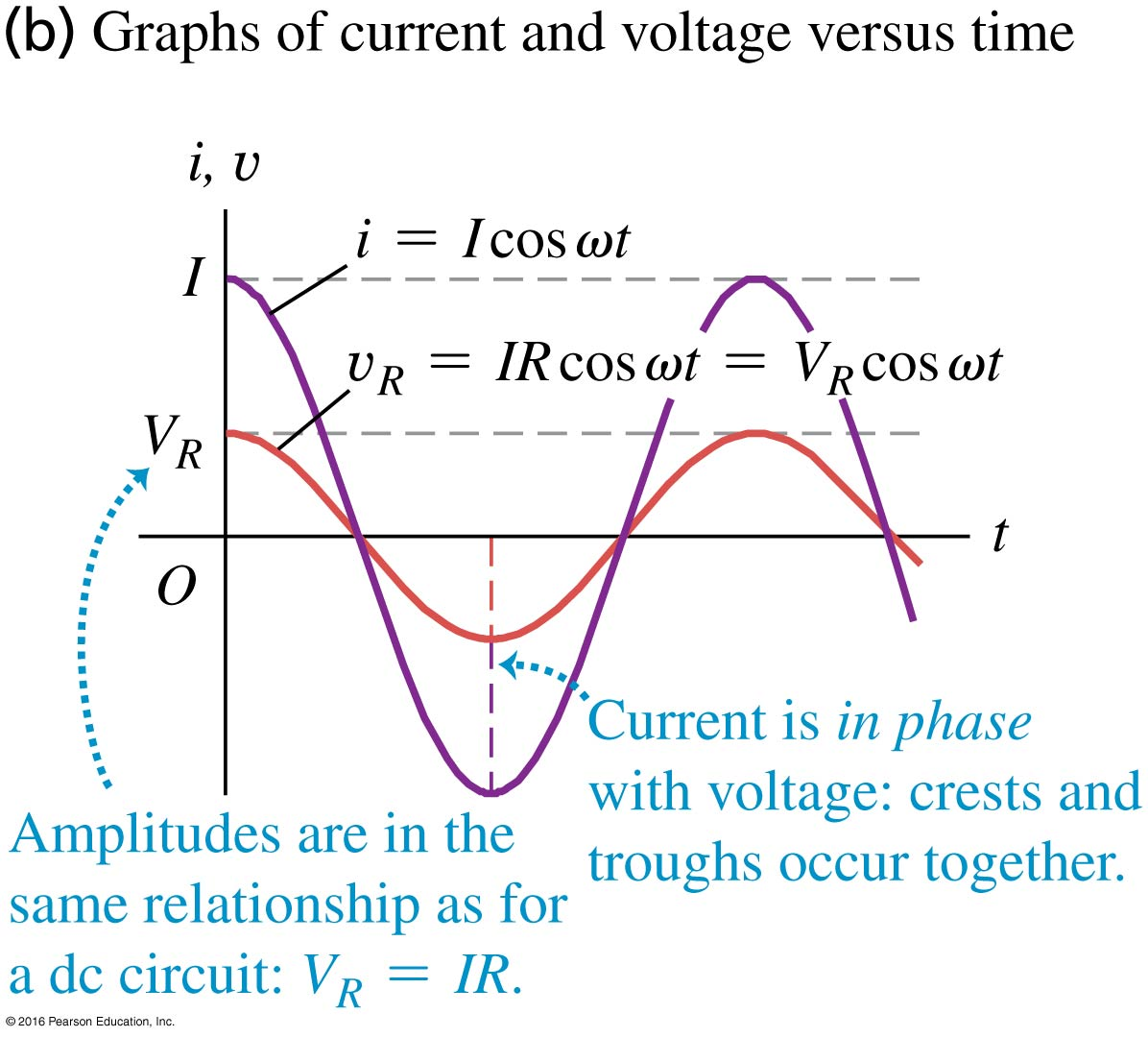
Figure (a) below shows a $RL$ circuit in which an AC power source causes the current to vary sinusoidally in time according to $i(t)=I\cos (\omega t)$.

The voltage across the inductor varies in time according to $v_L(t)=I\omega L\cos (\omega t+90^o)$.

The term $\omega L$ is called the inductive reactance: $X_L\equiv \omega L$, which has units of $\text{Ohms}$ when $L$ has units of $\text{H}$ and $\omega$ has units of $\text{rad}/\text{s}$. With this new variable, $v_L(t)=I{X}_L\cos (\omega t+90^{\circ })$.

Figure (b) shows the $v(t)$ and $i(t)$. The voltage across the inductor “leads” the current by $90^{\circ }$ (or, equivalently, $T/4$, where $T=2\pi /\omega$) because the maxima (or minima) in $v_L(t)$ occur before the maxima (or minima) in $i(t)$.

1.3 C Only

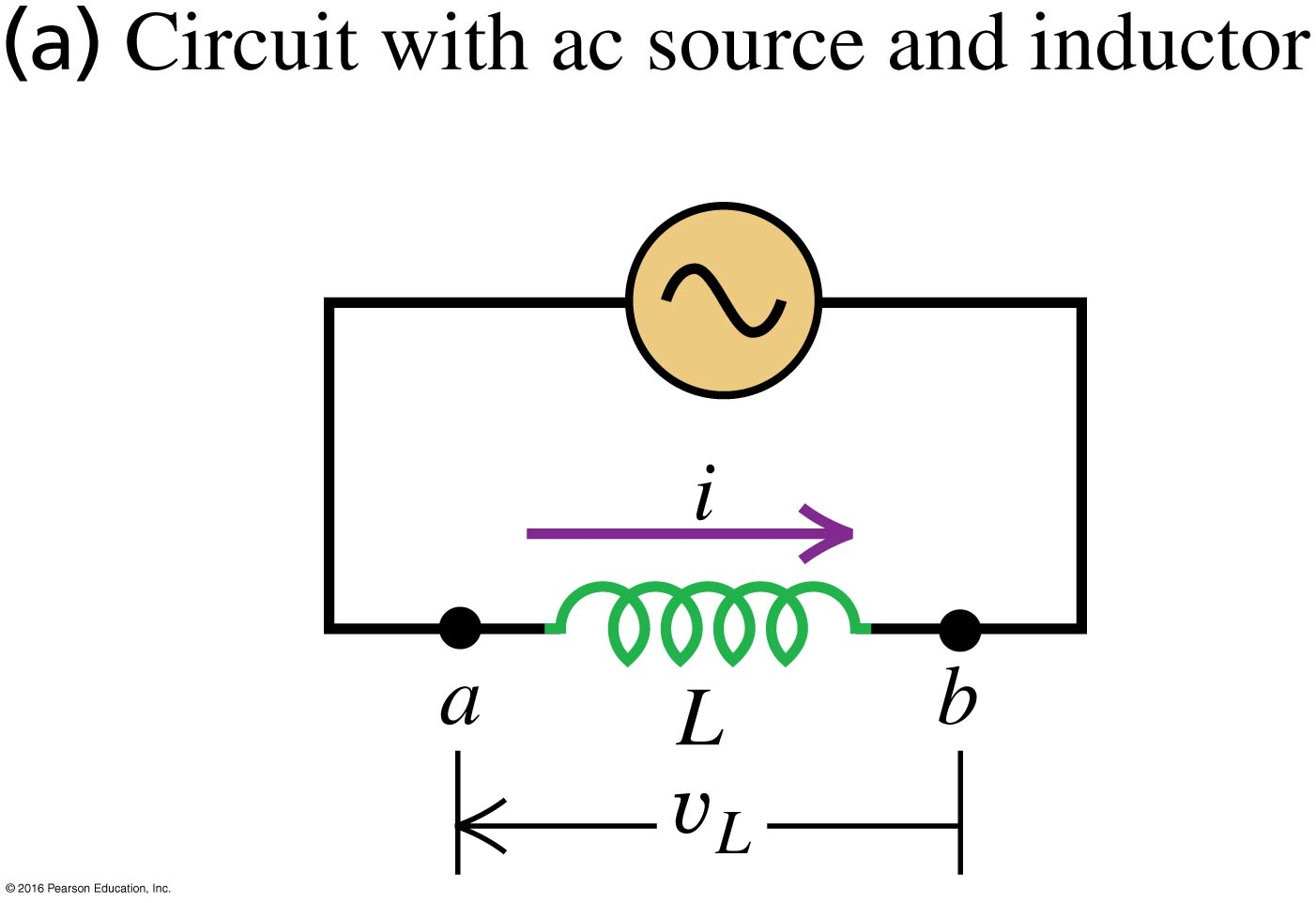
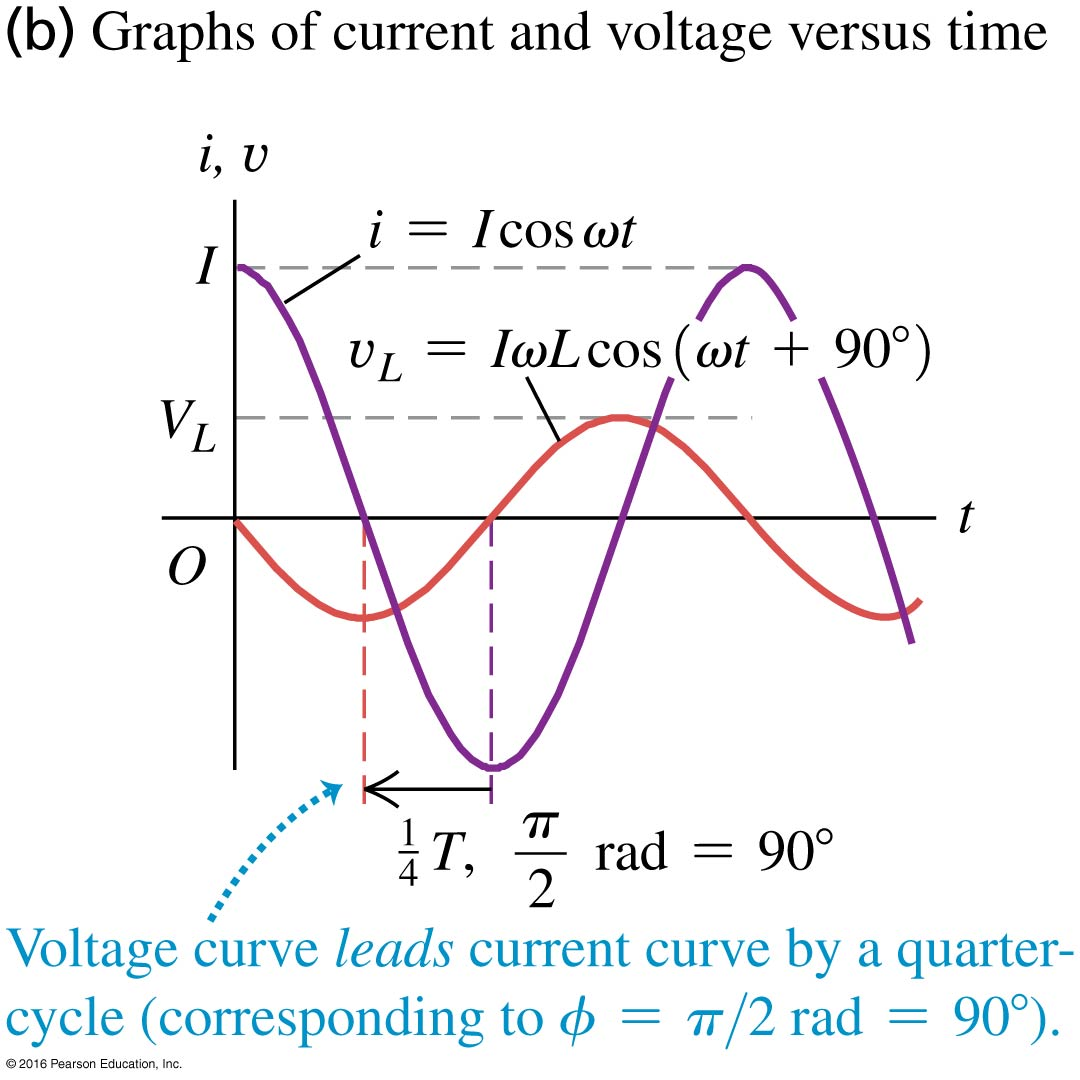
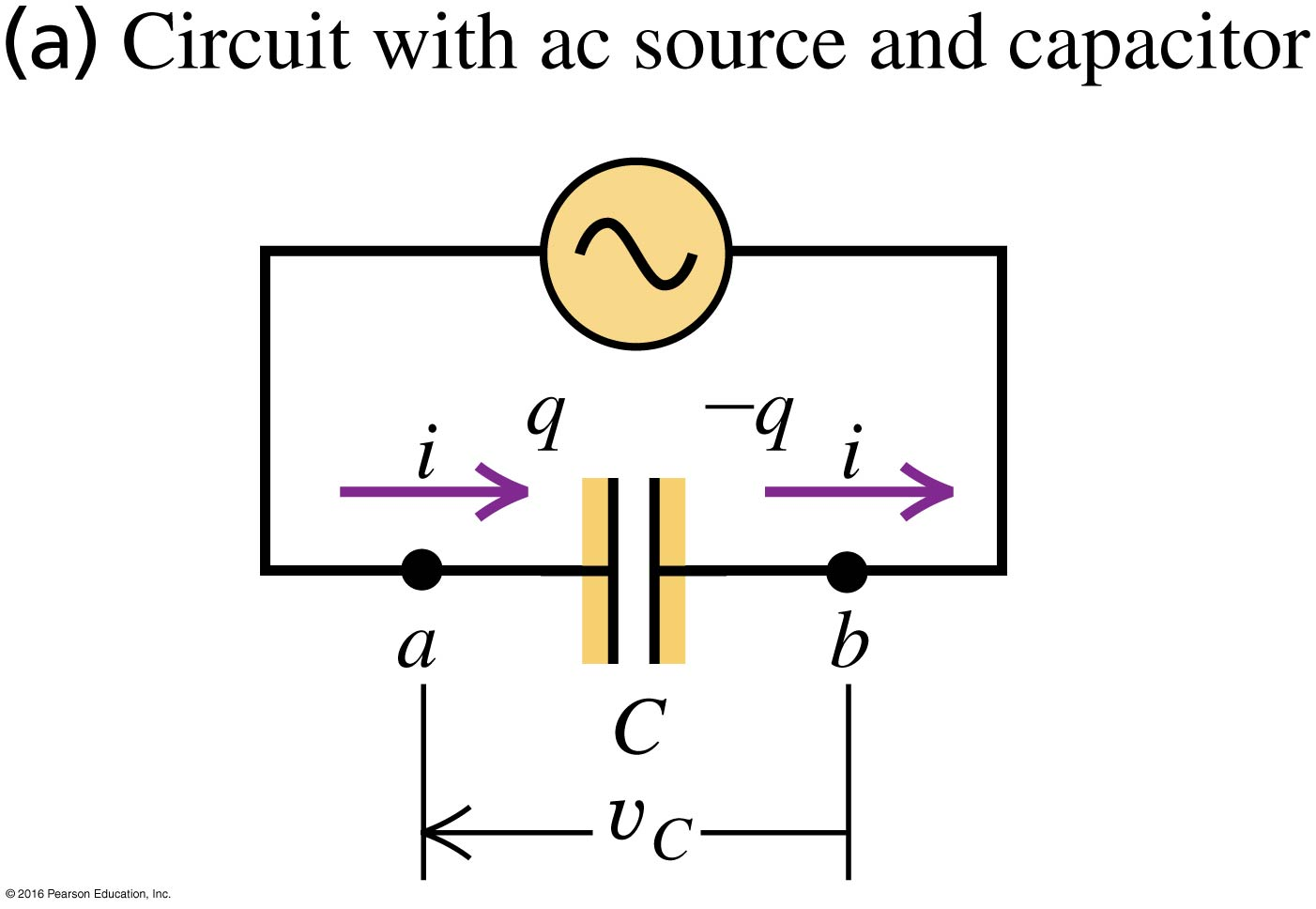
Figure (a) below shows a $RC$ circuit in which an AC power source causes the current to vary sinusoidally in time according to $i(t)=I\cos (\omega t)$.

The voltage across the capacitor varies according to $v_C(t)=\frac{I}{\omega C}\cos (\omega t-90^o)$.

The term $1/(\omega C)$ is called the capacitive reactance: $X_C\equiv 1/(\omega C)$. With this new variable, $v_C(t)=I{X}_C\cos (\omega t-90^{\circ })$.

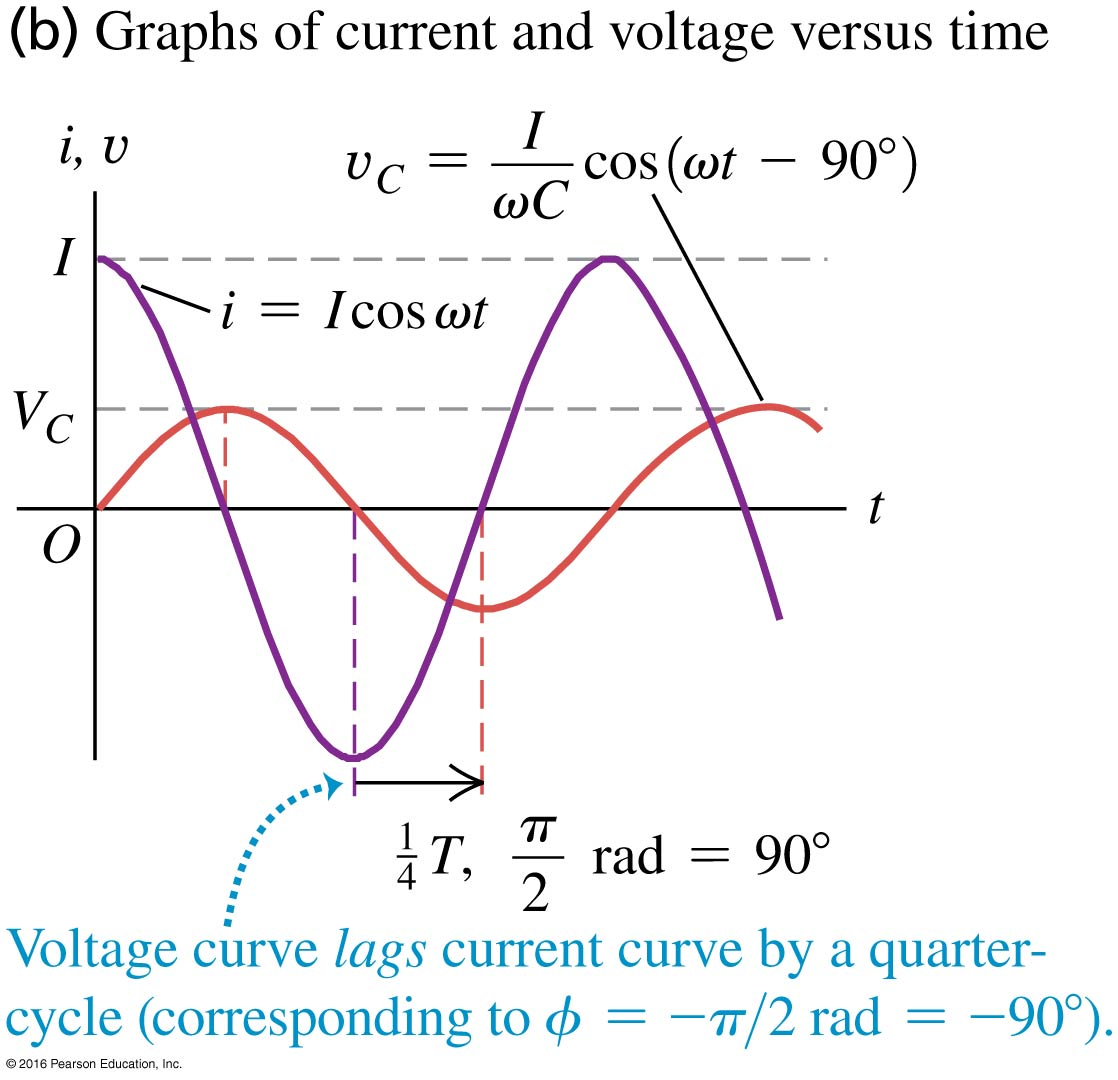
Figure (b) shows the $v(t)$ and $i(t)$. The voltage across the inductor “lags” the current by $90^{\circ }$ (or, equivalently, $T/4$) because the maxima (or minima) in $v_C(t)$ occur after the maxima (or minima) in $i(t)$.

1.4 Series LRC circuit

Suppose that we know the current $i(t)$ in the following series LRC circuit is $i(t)=I\cos (\omega t)$.

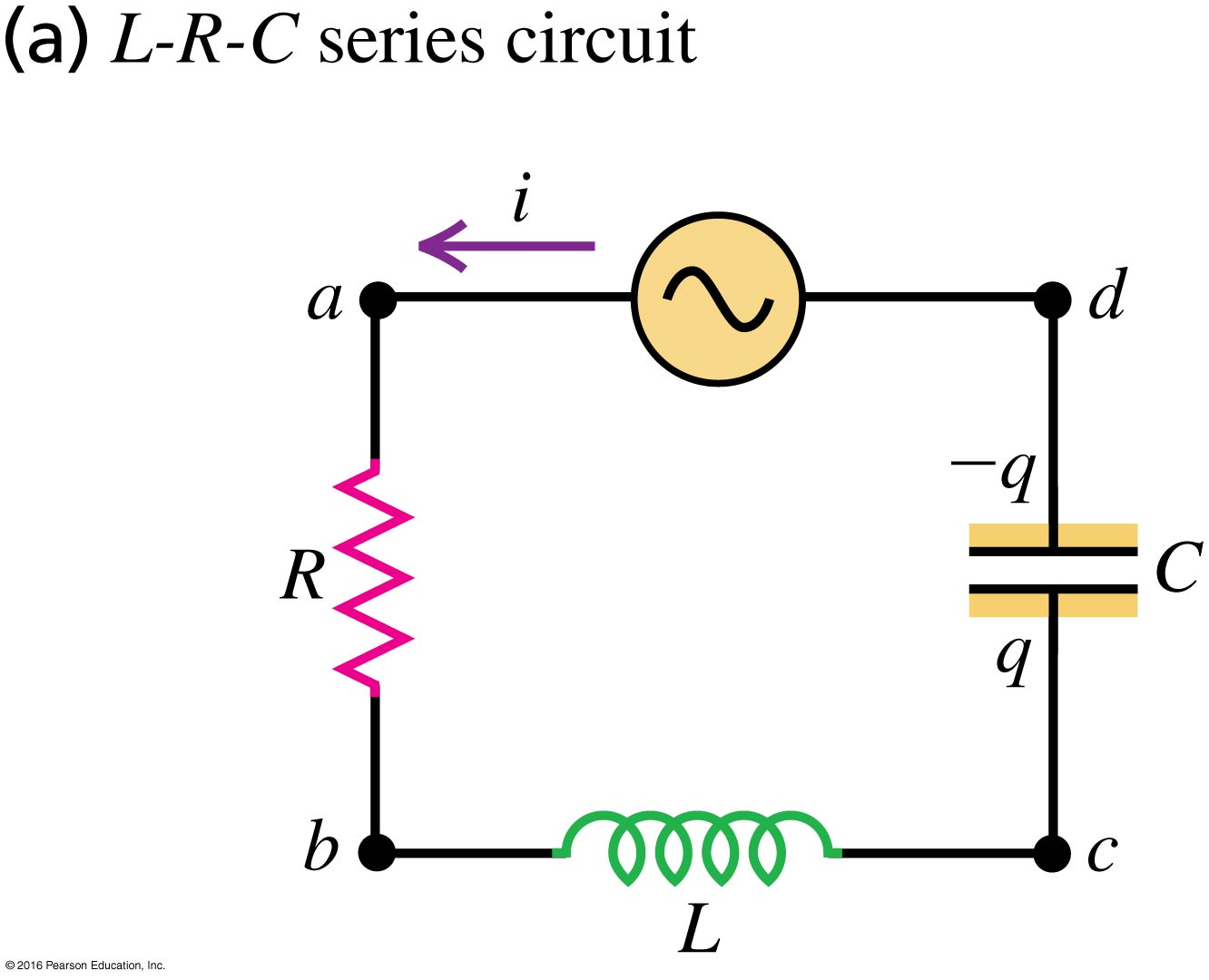
We want to know the voltage across the AC power supply, $v_d-v_a$, which we call $v$. We know the voltage across each of the components from the discussion above:

$$v_R(t)=IR\cos (\omega t)$$

$$v_L(t)=I\omega L\cos (\omega t+90^{\circ })=I{X}_L\cos (\omega t+90^{\circ })$$

$$v_C(t)=\frac{I}{\omega C}\cos (\omega t-90^{\circ })=I{X}_C\cos (\omega t-90^{\circ })$$

From Kirchhoff’s voltage law:

$$v(t)-v_R(t)-v_L(t)-v_C(t)$$

Substitution gives

$$v(t)=IR\cos (\omega t)+I{X}_L\cos (\omega t+90^{\circ })+I{X}_C\cos (\omega t-90^{\circ })$$

In this activity, you will compute $v(t)$ in two ways. First, you will use the above formula and a trig identity to write $v(t)$ in the form $IZ\cos (\omega t+\varphi )$, where the constants $Z$ and $\varphi$ depend on $R$, $L$, and $C$ (or equivalently, $R$, $X_L$, and $X_C$). Next, you will use a general formula to compute $Z$ and $\varphi$.

2 Problem I

A series LRC circuit with known values of $I$, $R$, $L$, and $C$ are such that $IR=1\text{ [V]}$, $I{X}_L=1\text{ [V]}$, and $X_C=0$. In addition, assume $i(t)=(1\text{ A})\cos \omega t$ and $\omega =2\pi {\text{ s}}^{-1}$.

Plot all quantities requested below on the same graph.

1. Plot $i(t)$

   108-109

   Answer: See Desmos plot

   110-113

2. Compute the period, $T$, of $i(t)$

   116-117

   Answer: There are two ways to answer this.

   1. The current is $i(t)=\cos \omega t$.

      • At $t=0\text{ s}$, $i(0\text{ s})=1$.

      • When $\omega t=2\pi \text{ s}$, $i(2\pi \text{ s})=1$ again for the first time.

        So the time for the $i(t)$ to return to its starting value is $t$ such that $\omega t=2\pi \Rightarrow t=2\pi /(2\pi {\text{ s}}^{-1})=1\text{ s}$.

   2. Using the formula $T=2\pi /\omega$.

   118-129

3. Plot $v_R(t)$, $v_L(t)$, and $v_C(t)$

   132-133

   Answer: See Desmos plot. Note that $v_C=0$ when $X_C=1/(\omega C)=0$. To get $X_C\approx 0$ in the Desmos plot, we set $C=1000$.

   134-137

4. Starting with $v(t)=v_R(t)+v_L(t)+v_C(t)$, use the trig identity

   140-141

   $A\cos (\theta )+B\cos (\theta +\pi /2)=\sqrt{A^2+B^2}\cos \left(\theta +{\tan }^{-1}(B/A)\right)$

   142

   to write $v(t)$ in the form $v(t)=Z\cos (\omega t+\varphi )$.

   144

   That is, find the constants $Z$ and $\varphi$.

   146

   Answer: Here we have $v_R(t)=\cos \omega t$, $v_L(t)=\cos (\omega t+\pi /2)$, and $v_C(t)=0$, so

   $v(t)=\cos \omega t+\cos (\omega t+\pi /2)$.

   This matches the given identity if $A=B=1$, so

   $v(t)=\sqrt{2}\cos (\omega t+{\tan }^{-1}(1/1))=\sqrt{2}\cos (\omega t+\pi /4)$.

   Because of the $+\pi /4$, we say that $v(t)$ leads $i(t)$ by $\pi /4$ (or $45^{\circ }$ or $T/8$).

   148-159

5. Plot $v(t)$

   162-163

   Answer: See Desmos plot. Adjust the parameters $R$, $L$, and $C$ to see how they change the curves (amplitudes and phases).

    

   164-167

3 Problem II

In the previous problem, computing $v(t)$ required the use of a trig identity to combine $v_R$ and $v_L$ and write $v(t)$ in the form $v(t)=Z\cos (\omega t+\varphi )$, where $Z$ and $\varphi$ are constants that depend on $L$ and $R$. When $v_C$ is not zero, additional algebra is needed to compute $v(t)$ (by using the trig identity again). However, there is a formula that can be used to find $v(t)$ in general so that trig identities are not needed.

It can be shown that in general, the voltage across the AC power source in a RLC circuit when $i(t)=I\cos \omega t$ is

$$v(t)=IZ\cos (\omega t+\varphi )$$

Where the series LRC impedance $Z$ is defined as

$$Z=\sqrt{R^2+(X_L-X_C{)}^2}$$

and

$$\varphi ={\tan }^{-1}\left(\frac{X_L-X_C}{R}\right)={\tan }^{-1}\left(\frac{\omega L-\frac{1}{\omega C}}{R}\right)$$

When $\varphi$ is positive, $v(t)$ leads $i(t)$. When $\varphi$ is negative, $v(t)$ lags $i(t)$. When $\varphi =0$, $v(t)$ is in phase with $i(t)$.

1. Using the parameters given in the previous problem, find $v(t)$ using the above formula.

   194-195

   Answer: In the previous problem, we were given $I=1\text{ [A]}$, $IR=1\text{ [V]}$, so $R=1\Omega$. Thus

   $$Z=\sqrt{R^2+(X_L-X_C{)}^2}=\sqrt{((1\Omega {)}^2+(1\Omega -0{)}^2}=\sqrt{2}\Omega$$

   and

   $$\varphi ={\tan }^{-1}\left(\frac{X_L-X_C}{R}\right)={\tan }^{-1}\left(\frac{1-0}{1}\right)={\tan }^{-1}\left(\frac{1}{1}\right)=\frac{\pi }{4}$$

   Thus,

   $$v(t)=IZ\cos (\omega t+\varphi )=(\sqrt{2}\text{ [V]})\cos (\omega t+\pi /4)$$

   which is the same as found in the previous problem.

   196-219

2. Suppose $X_C$ is not zero. What is the relationship between $\omega$, $L$, and $C$ such that the voltage and current in the circuit is in phase?

   222-223

   Answer: The voltage varies according to $v(t)=IZ\cos (\omega t+\varphi )$, where $\varphi ={\tan }^{-1}\left(\frac{\omega L-\frac{1}{\omega C}}{R}\right)$.

   The voltage is in phase with the current, which varies according to $i(t)=I\cos (\omega t)$, when $\varphi =0$. This requires

   $\frac{\omega L-\frac{1}{\omega C}}{R}=0$, or ${\omega }^2=LC$.

   224-231